Multivariate multi-step time series forecasting using sequence models (1/4)

Photo by Nathan Dumlao on Unsplash

While working on a multivariate multi-step time series forecasting problem, I couldn’t find any awesome techniques/models.

Then, I remembered having worked earlier on a personal project, where I was using sequence models like an encoder-decoder to do machine translation.

If you think about it, machine translation is also very similar to multivariate multi-step time series forecasting. Both have 3D input and 3D output.

But, there are a couple of differences -

1. There are no word embeddings or an embedding layer.
2. The input and output sequence length remains the same, unlike machine translation where the sentences can be of any length up-to a maximum length.
3. There are no special tokens like <start>, <end> and <pad>.

For eg , an English to Italian input-output mapping looks like -

Input Language; index to word mapping
1 ----> <start>
4 ----> i
155 ----> broke
7 ----> it
3 ----> .
2 ----> <end>
0 ----> <pad>
0 ----> <pad>
0 ----> <pad>

Target Language; index to word mapping
1 ----> <start>
24 ----> l
11 ----> ho
425 ----> rotto
3 ----> .
2 ----> <end>
0 ----> <pad>
0 ----> <pad>
0 ----> <pad>
0 ----> <pad>
0 ----> <pad>

Before going to the models, I’m going to briefly touch on a few concepts.

Existing encoder-decoder architectures

• A

Pictorially, an encoder-decoder model looks like -

credit — https://www.baeldung.com/cs/nlp-encoder-decoder-models

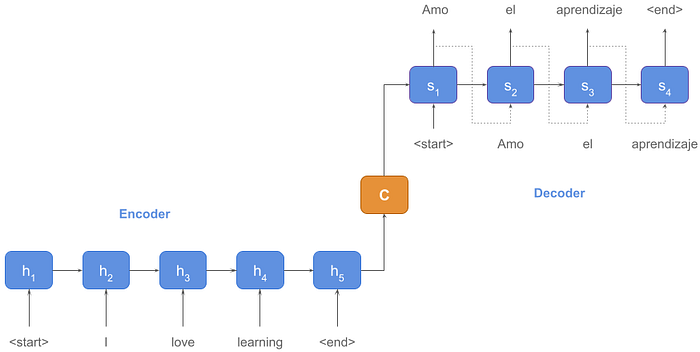
At the decoder side, at every time step the decoder layer is fed with the model’s output at the previous time step.

But, most of the implementations are not a true representation of this image. They make use of another concept called Teacher forcing.

Teacher forcing works by using the actual or expected output from the training dataset at the current time step y(t) as input in the next time step X(t+1), rather than the output generated by the network.

The model is trained given source and target sequences where the model takes both the source and a shifted version of the target sequence as input and predicts the whole target sequence.

For eg —

Train code -

# returns train, inference_encoder and inference_decoder models
def define_models(n_input, n_output, n_units):
 # define training encoder
 encoder_inputs = Input(shape=(None, n_input))
 encoder = LSTM(n_units, return_state=True)
 encoder_outputs, state_h, state_c = encoder(encoder_inputs)
 encoder_states = [state_h, state_c]
 # define training decoder
 decoder_inputs = Input(shape=(None, n_output))
 decoder_lstm = LSTM(n_units, return_sequences=True, return_state=True)
 decoder_outputs, _, _ = decoder_lstm(decoder_inputs, initial_state=encoder_states)
 decoder_dense = Dense(n_output, activation='softmax')
 decoder_outputs = decoder_dense(decoder_outputs)
 model = Model([encoder_inputs, decoder_inputs], decoder_outputs)
 # define inference encoder
 encoder_model = Model(encoder_inputs, encoder_states)
 # define inference decoder
 decoder_state_input_h = Input(shape=(n_units,))
 decoder_state_input_c = Input(shape=(n_units,))
 decoder_states_inputs = [decoder_state_input_h, decoder_state_input_c]
 decoder_outputs, state_h, state_c = decoder_lstm(decoder_inputs, initial_state=decoder_states_inputs)
 decoder_states = [state_h, state_c]
 decoder_outputs = decoder_dense(decoder_outputs)
 decoder_model = Model([decoder_inputs] + decoder_states_inputs, [decoder_outputs] + decoder_states)
 # return all models
 return model, encoder_model, decoder_model

Inference code -

# generate target given source sequence
def predict_sequence(infenc, infdec, source, n_steps, cardinality):
 # encode
 state = infenc.predict(source)
 # start of sequence input
 target_seq = array([0.0 for _ in range(cardinality)]).reshape(1, 1, cardinality)
 # collect predictions
 output = list()
 for t in range(n_steps):
 # predict next char
 yhat, h, c = infdec.predict([target_seq] + state)
 # store prediction
 output.append(yhat[0,0,:])
 # update state
 state = [h, c]
 # update target sequence
 target_seq = yhat
 return array(output)

Here, during training, the decoder lstm is initialized with shape (None,None,features) and return_sequences=True .

The time steps dimension is initialized with None, ie its variable in length. Within a single batch, you must have the same number of timesteps, but between batches there is no such restriction. Thus, we can pass and receive different time steps from the decoder during training and inference.

This is important, because during inference, before the decoding process starts, the only thing that we have are the last hidden and cell states from the encoder. Thus, we can’t pass multiple input values to the decoder in one single shot, so we pass and receive 1 time step from the decoder in a loop during inference.

Although teacher forcing is a great technique which provides a fast and effective way to train a recurrent neural network that uses output from prior time steps as input to the model.

But, the approach can also result in models that may be fragile or limited when used in practice when the generated sequences vary from what was seen by the model during training.

During inference, the model now must predict longer sequences, and can no longer rely on the frequent corrections. In each step, the last prediction is appended as new input for the next step. Hereby, minor mistakes that were not critical during training amplify over longer sequences during inference.

• B

Another similar approach has a decoder but with fixed time steps, for eg let’s say the decoder lstm is initialized with shape (None,5,features).

Now, with this approach, we can’t pass and receive different time steps from the decoder during training and inference.

The training process is similar to the previous model, but the difference comes during inference where we now need to pass 5 input values to the decoder in one single shot.

For this model to work, the last hidden state returned by the encoder is passed to a repeat vector layer to generate multiple inputs which are passed to the decoder in one single shot during inference.

Here, during training, this is what happens at the decoder side -

T9 --> T10

T10 --> T11

T11 --> T12

T12 --> T13

T13 --> T14

And during inference -

T9 --> T10

T9 --> T11

T9 --> T12

T9 --> T13

T9 --> T14

During training, at each time step, we feed the Tth value to the decoder and expect T+1th value as output from the network.

But, during inference, at each time step, we feed the same value to the decoder and expect different values as output from the network.

Thus, this model is also not a true representation of the encoder-decoder model.

• C

Another implementation that is widely used doesn’t even make use of a decoder input.

credit — https://stackoverflow.com/questions/51749404/how-to-connect-lstm-layers-in-keras-repeatvector-or-return-sequence-true

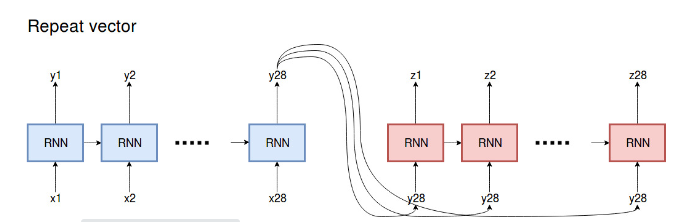
In this approach, the encoder lstm is initialized with return_states=False and return_sequences=False, ie it only returns the last hidden state.

The last hidden state is passed to each time step of the decoder using a repeat vector layer.

In this case, the decoder neither makes use of teacher forcing nor the output from prior time steps as input.

In time series forecasting problems where the input/output windows are large, for eg forecasting sales of a retail store for the next three months, this would be a bottleneck.

Code -

 # define model
 model = Sequential()
 model.add(LSTM(200, activation='relu', input_shape=(n_timesteps, n_features)))
 model.add(RepeatVector(n_outputs))
 model.add(LSTM(200, activation='relu', return_sequences=True))
 model.add(TimeDistributed(Dense(100, activation='relu')))
 model.add(TimeDistributed(Dense(1)))
 model.compile(loss='mse', optimizer='adam')
 # fit network
 model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)

Keeping all these things in mind, I have written a few custom models of my own, blending NLP and time series concepts, which can be used for univariate/multivariate multi-step time series forecasting problems.

• All parts

Part — 1

Part — 2

Part — 3

Part — 4

• Github & Linkedin

GitHub — pc90/Multivariate-multi-step-time-series-forecasting-using-sequence-models

https://www.linkedin.com/in/puneet-chandna-050486131/

• References

Neural Machine Translation by Jointly Learning to Align and Translate

Effective Approaches to Attention-based Neural Machine Translation

Scheduled Sampling for Sequence Prediction with Recurrent Neural Networks

https://machinelearningmastery.com/teacher-forcing-for-recurrent-neural-networks/

https://machinelearningmastery.com/develop-encoder-decoder-model-sequence-sequence-prediction-keras/

https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/

https://machinelearningmastery.com/return-sequences-and-return-states-for-lstms-in-keras/

Training an RNN with examples of different lengths in Keras

How to connect LSTM layers in Keras, RepeatVector or return_sequence=True?

Seq2Seq with Attention and Beam Search

Making new Layers and Models via subclassing | TensorFlow Core

Neural machine translation with attention | Text | TensorFlow

Applied Roots