Multivariate multi-step time series forecasting using sequence models (3/4)

Photo by Jack Sharp on Unsplash

Models -

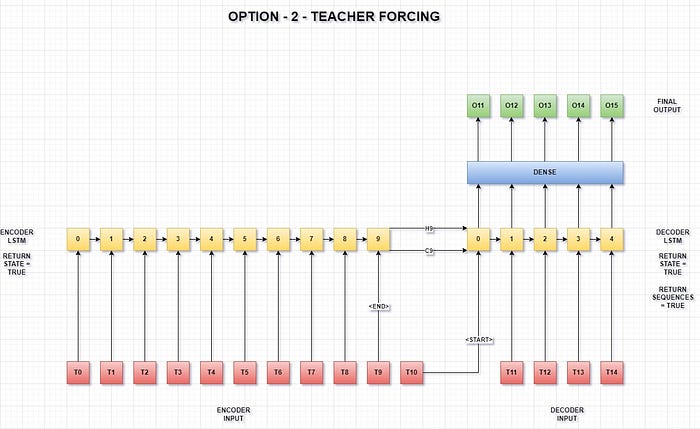
Option — 2

In this approach, the second last time step of the encoder input is used as the <end> token for the encoder and the last time step of the encoder input is used as the <start> token for the decoder.

The number of encoder input time steps is one more than option-1 for easy visualization and fair comparison.

• Teacher forcing with shared weights

In this model, we use teacher forcing to create an encoder-decoder model.

The model architecture looks like -

Image by author

Train code -

Inference code -

Teacher forcing with shared weights and Luong’s Dot Attention

Although, it doesn’t make much sense to have attention in a time series forecasting problem, as in most of the cases the attention would be on the last few time time steps only which the context vector is able to capture to a certain extent, but I have written the attention models just out of curiosity.

Also, I’m guessing the input feeding mechanism only further confuses the time series models.

The Dot attention mechanism can be explained as —

Let n_in = 10 and units/hidden size = 256

Encoder hidden states = Hen = (None,10,256)
Decoder hidden states at each decoder time step = Hd = (None,256)
Hd = tf.expand_dims(Hd,1) = (None,1,256)

So,

score = Hen.Hd.T
score = (None,10,256).(None,1,256).T
score = (None,10,256).(None,256,1)
score = (None,10,1)

attention_weights = tf.nn.softmax(score, axis=1) = (None,10,1)

context_vector = attention_weights * Hen
context_vector = (None,10,1) * (None,10,256)
context_vector = (None,10,256)

context_vector = tf.reduce_sum(context_vector, axis=1)
context_vector = (None,256)

This context vector is concatenated 
with the input at each time step at the decoder side.

Train code -

Inference code -

• Teacher forcing with shared weights and Luong’s General Attention

The General attention mechanism can be explained as —

Let n_in = 10 and units/hidden size = 256

Encoder hidden states = Hen = (None,10,256)
Decoder hidden states at each decoder time step = Hd = (None,256)
Hd = tf.expand_dims(Hd,1) = (None,1,256)
Trainable matrix Wa = (None,Encoder hidden size,Decoder hidden size)
Trainable matrix Wa = (None,256,256)

So,

score = Hen.Wa
score = (None,10,256).(None,256,256)
score = (None,10,256)

score = score.Hd.T
score = (None,10,256).(None,1,256).T
score = (None,10,256).(None,256,1)
score = (None,10,1)

attention_weights = tf.nn.softmax(score, axis=1) = (None,10,1)

context_vector = attention_weights * Hen
context_vector = (None,10,1) * (None,10,256)
context_vector = (None,10,256)

context_vector = tf.reduce_sum(context_vector, axis=1)
context_vector = (None,256)

This context vector is concatenated 
with the input at each time step at the decoder side.

Train code -

Inference code -

• Teacher forcing with shared weights and Luong’s Concat Attention

The Concat attention mechanism can be explained as —

Let n_in = 10 and units/hidden size = 256

Encoder hidden states = Hen = (None,10,256)
Decoder hidden states at each decoder time step = Hd = (None,256)
Hd = tf.expand_dims(Hd,1) = (None,1,256)
Trainable matrix W1 = (None,hidden size,Downsample)
Trainable matrix W1 = (None,256,128)
Trainable matrix W2 = (None,hidden size,Downsample)
Trainable matrix W2 = (None,256,128)
Trainable matrix V = (None,1,hidden size)
Trainable matrix V = (None,1,256)

So,

enc_w1 = Hen.W1
enc_w1 = (None,10,256).(None,256,128)
enc_w1 = (None,10,128)

dec_w2 = Hd.W2
dec_w2 = (None,1,256).(None,256,128)
dec_w2 = (None,1,128)
dec_w2 = tf.broadcast_to(dec_w2, tf.shape(enc_w1))
dec_w2 = (None,10,128)

score = tf.math.tanh(tf.concat([enc_w1, dec_w2], axis=-1))
score = (None,10,256)
score = score.V.T
score = (None,10,256).(None,1,256).T
score = (None,10,256).(None,256,1)
score = (None,10,1)

attention_weights = tf.nn.softmax(score, axis=1) = (None,10,1)

context_vector = attention_weights * Hen
context_vector = (None,10,1) * (None,10,256)
context_vector = (None,10,256)

context_vector = tf.reduce_sum(context_vector, axis=1)
context_vector = (None,256)

This context vector is concatenated 
with the input at each time step at the decoder side.

Train code -

Inference code -

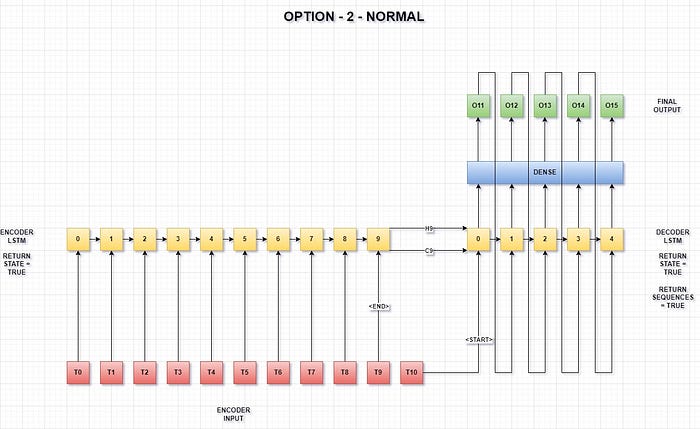
• Without teacher forcing with shared weights

In this model, we use output from prior time steps as input to the decoder to create an encoder-decoder model.

The model architecture looks like -

Image by author

Train code -

Inference code -

• Without teacher forcing with shared weights and Luong’s Dot Attention

Train code -

Inference code -

• Without teacher forcing with shared weights and Luong’s General Attention

Train code -

Inference code -

• Without teacher forcing with shared weights and Luong’s Concat Attention

Train code -

Inference code -

• Teacher forcing with separate weights

In machine translation, we have sentences which are converted into vector embeddings by the embedding layer.

But, in time series data, we don’t have such complexities, each parallel time series corresponds to one single feature of each layer’s third dimension.

In this model, we use teacher forcing along with separate encoder, decoder and dense layers for each time series to create an encoder-decoder model. Accordingly the training time and the number of parameters increase proportionately with the number of features.

This one model is equivalent to having a separate model for each of your time series data. Thus, this model should be used when accuracy is of utmost importance.

Also, even though it’s very easy to add attention to the separate models as well, I’ve left that out, because it further increases the training time.

Train code -

Inference code -

• Without teacher forcing with separate weights

In this model, we use output from prior time steps as input to the decoder along with separate encoder, decoder and dense layers for each time series to create an encoder-decoder model.

Train code -

Inference code -

• Teacher forcing with hybrid weights

In this approach we create a hybrid model, combining both shared and separate models for a specific use case.

Let’s say we are working on an IOT application, where we have multiple sensors of various kinds.

For eg -

1. The first 10 time series are a measurement of temperature at various places in a smart building.
2. The next 10 time series are a measurement of the amount of light entering the smart building at various places.
3. The next 2 time series are a measurement of some quantity ‘x’.
4. The next 1 time series is a measurement of some quantity ‘y’.
5. The next 1 time series is a measurement of some quantity ‘z’.

Here, we create a model with compartmentalized-sharing of weights, ie -

1. The first 10 time series share weights only with each other.
2. The next 10 time series share weights only with each other.
3. The next 2 time series share weights only with each other.
4. The next 1 time series has it’s own weights.
5. The next 1 time series has it’s own weights.

Thus, with this model we strive to strike a balance between faster training and accuracy by combining the best of both worlds.

Again, even though it’s very easy to add attention to the hybrid models as well, I’ve left that out, because it further increases the training time.

NOTE : The results from the notebook do not reflect this scenario as this is just an example. If you’re working on something similar, then you need to alter the code according to your dataset.

Train code -

Inference code -

• Without teacher forcing with hybrid weights

Train code -

Inference code -

• All parts

Part — 1

Part — 2

Part — 3

Part — 4

• Github & Linkedin

GitHub — pc90/Multivariate-multi-step-time-series-forecasting-using-sequence-models

https://www.linkedin.com/in/puneet-chandna-050486131/

• References

Neural Machine Translation by Jointly Learning to Align and Translate

Effective Approaches to Attention-based Neural Machine Translation

Scheduled Sampling for Sequence Prediction with Recurrent Neural Networks

https://machinelearningmastery.com/teacher-forcing-for-recurrent-neural-networks/

https://machinelearningmastery.com/develop-encoder-decoder-model-sequence-sequence-prediction-keras/

https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/

https://machinelearningmastery.com/return-sequences-and-return-states-for-lstms-in-keras/

Training an RNN with examples of different lengths in Keras

How to connect LSTM layers in Keras, RepeatVector or return_sequence=True?

Seq2Seq with Attention and Beam Search

Making new Layers and Models via subclassing | TensorFlow Core

Neural machine translation with attention | Text | TensorFlow

Applied Roots